Метод решения кубического уравнения.

 

 

 

Данное уравнение можно представить в виде выражения:

 

Приравнивая коэффициенты при равных степенях x , имеем:

 

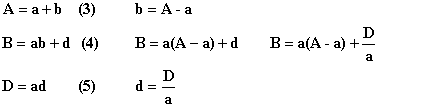
Уравнение (1) имеет 3 корня, причём 1 корень всегда действительный, а два других могут быть как действительными, так и комплексными (мнимыми). Нахождение корней уравнения (1) возможно с использованием формулы Кардано, но необходимо использовать комплексные числа и гиперболические функции.

При использовании разложения (2) не требуется использование комплексных чисел, все коэффициенты a, b, d – числа действительные.

Нахождение корней уравнения (2) производится по формулам:

 

    

 

Вычисление коэффициентов a, b, d возможно решением системы уравнений (3), (4), (5).

Если уравнение (1) имеет 3 действительных корня, то коэффициенты a, b, d имеют по 3 значения каждый, если уравнение (1) имеет только один действительный корень, то возможно единственное разложение и единственное значение коэффициентов a, b, d.

Решение системы уравнений (3), (4), (5) возможно путём приближений подстановкой вместо коэффициента a предполагаемого числа.

Если задано число а , то остальные коэффициенты высчитываются по формулам:

   (7)

Проверка верности решения производится по формуле (4) .

Для ускорения решения необходимо вычислить предварительное значение a , близкое к фактическому.

Из уравнения получается:

 

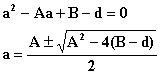
Поскольку  a  – всегда действительное число, то подкоренное выражение всегда .

                     

 

Если подкоренное выражение обозначить как n² , то получится:

               (8)           

 

    (9)                        (10)

 

            (11)

 

Если коэффициенты A, B, D и корни уравнения – целочисленные, то число n тоже имеет целочисленное значение, и подбором n (начиная с нуля) можно достичь выполнения равенства (10).

Для определения корней достаточно найти одно значение d .

Из уравнения (4), (5), (6) получается:

 

                (12)

 

                 (13)     (14)

 

 , то      при  D > 0;        при   D < 0                    (15)

 

    (16)       

 

При целочисленных  значениях  a, d, D значения  a, d  подбираются из значений делителей числа D.

 

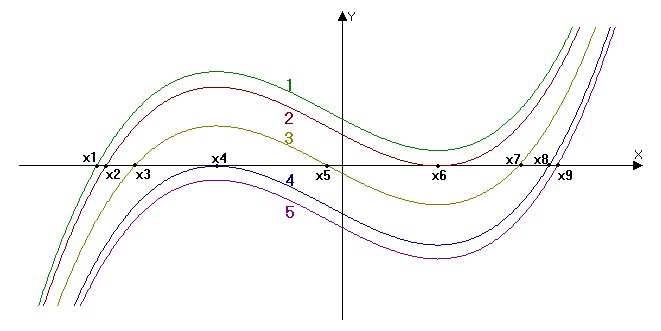
Рассмотрим графики уравнения (1) при разных значениях коэффициента D .

 

N графика	Корни уравнения	D
1 2 3   4 5	x1, два корня комплексные (мнимые) x2,   x6 – двойной, (правый) x3, x5, x7;  - точка перегиба x4 – двойной (левый),   x8 x9 ; два корня комплексные (мнимые)	D1 D2 D3   D4 D5

 

Коэффициенты D₂ ,  D₃ ,  D₄  можно точно подсчитать и, сравнивая коэффициент  D  заданного уравнения с D₂ ,  D₃ ,  D₄ , можно оценить значения корней уравнения.

 

График 2

                    или      a  >  е_п

(17)

   

 

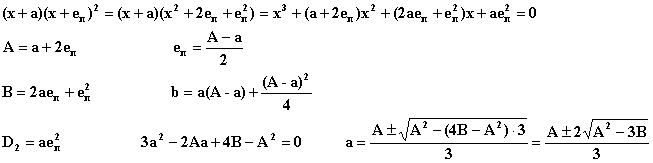
      Учитывая, что е_п <  a , расставаляем знаки

   (18)               (19)  

 

           (20)  формула Хайретдинова-Мусина

           

График 3

                   (21)

        

        (22)                   

  (23)                

Учитывая, что x₃<x₇        (24)

   (25)             (26)

               

 

                 >0 , то возможен двойной корень справа

Если (26) =0 , то корень x₅ в точке перегиба

                 <0 , то возможен двойной корень слева

 

График 4

Левый двойной корень x₄ и одиночный корень x₈

A=2а_л + е_л

             

 

 

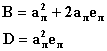
   (27)               (28)

    (29)     формула Хайретдинова-Мусина

 

Случаи, когда A²-3B <0.

 

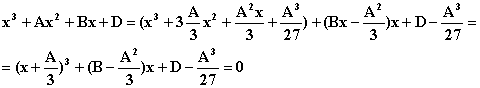
При A²-3B =0 

В случае, когда одновременно выполняется A²=3B и  получается уравнение с тройным корнем

           

При A²=3B , но    получается уравнение 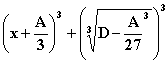  т.к. по формуле разложения суммы кубов получаем вещественный корень, равный

   (30)

Остальные корни х₂ ,х₃ высчитываются по обычным формулам как мнимые корни.

При A² < 3B корень х₁ находится, опираясь на формулу (30).

24.08.2003

Подбор приближённого значения корня уравнения (1) и пример