Из (13) и (14) вытекает, что d = M – g = M -    (16)

Из формул (12) и (15) видно, что k² = n² , поэтому A² – 4B + 4(d+g) = A² –  

После преобразований и учитывая (13) имеем     – 4B + 4M = -

m² = 4D(M - B) + E²       (17)

Из (12) и (8) имеем: b = A – a =      (18)

Из (17) и (8) имеем  ab =             (19)

Подставив решения уравнения (10) и (11) в уравнение (6) , получаем E = a ·  ,

и для получения тождества необходимо, чтобы перед коэффициентом  m  стояли знаки   , поэтому формулы для d и g перепишем в виде  d =  (20)   g =  (21) .

Взяв произведение dg , имеем, учитывая (7) :    dg = D =  , отсюда ab =   (22) .

Подставим в (12), (17) и (18) формулу (6) с учётом всех возможных сочетаний  имеем:

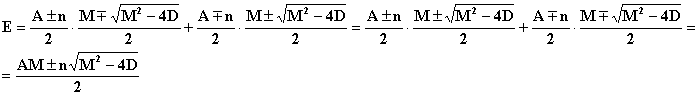
2E = AM     (23)     Вывод: при подстановке коэффициентов в формулу (23) в дальнейшем используется при вычислении g (16) тот знак при n , который удовлетворяет равенству (23) .

Заметим, что в формуле (23) выражение M² – 4D > 0 или |M| > 2 (24) при D > 0 , а при D < 0                  M² всегда > 4D.  Подставляя (13) в формулу M² > 4D , имеем: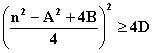

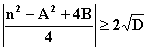      Решение этого неравенства  (25)    (26)

Учитывая формулы (8), (13), (20), (21) получаем: d + g = M =

4abM = 2a(E

Принимая во внимание (19) и (4) имеем: (A² – n²)M = 2EA ± 2m(a – b) , отсюда

m =   (27)

Знак числа m, полученный при вычислении по формуле (27) используется при вычислении d  (формула 20)

 

Алгоритм решения уравнения (1) по полученным формулам

Используя (24), (25), (26) определяем допустимые значения |M| и n .

Используем формулу (13) и составляем таблицу значений n , M , являющихся возможными участниками решений. Полученные значения n и М проверяем подстановкой в формулу (23), при выполнении равенства (23) эти числа n и M являются участниками решений. Знак при n учитывается при вычислении g по формуле (14).

Следует заметить, что для получения решений уравнения (1) достаточно вычислить один набор коэффициентов a, b, d, g, по которым можно вычислить согласно уравнению (2) все корни уравнения (1) и остальные наборы коэффициентов a, b, d, g (при необходимости).

Также следует заметить, что наборов коэффициентов a, b, d, g при наличии действительных корней обоих квадратных уравнений, составляющих уравнение (2) , будет существовать всего шесть (с учётом того, что квадратные уравнения в уравнении (2) можно поменять местами и обозначения a, b, d, g можно присвоить как, начиная с первого квадратного уравнения, так и начиная со второго квадратного уравнения).

При мнимых же корнях хотя бы одного квадратного уравнения в уравнения (2) наборов коэффициентов a, b, d, g будет существовать только два (с учётом перестановки квадратных уравнений). Вышесказанное наглядно видно из примера, представленного ниже:

                                                         a      d            b      g              a     d           b      g    

(x + 5)(x + 3)(x – 2)(x – 4) = ( x² + 8x + 15)(x² – 6x + 8) = (x² – 6x + 8)( x² + 8x + 15) = (x² + 3x – 10)(x² – x –12) =

= (x² – x –12) (x² + 3x – 10) = (x² + x – 20)(x² + x – 6) = (x² + x – 6)(x² + x – 20) = x⁴ +2x³ – 25x² – 26x + 120 = 0

 

Далее вычисляем значения а и b согласно формулам (12) и (18), при чём для (12) принимаем значения   + n ,

а для (18)  « – n » .

Далее алгоритм решения может продолжаться по двум ветвям. При первой ветви вычисление значения d и g производится по формуле (14) , причём знак при вычислении  g  берётся из формулы (23) , полученной при подстановке n и М и выполнении равенства (23).

При выполнении решения по второй ветви вычисляется коэффициент m по формуле (27) и определяется значения  d и g  по формулам  (20) и (21). Знак числа m по формуле (27) сохраняется при вычислении d (20).

Нужно проверить выполнение равенств (4), (5), (6), (7) подстановкой вычисленных коэффициентов a, b, d, g в эту систему уравнения. При выполнении равенств (4), (5), (6), (7) решение правильно и закончено.

16.09.2003